(本小题满分12分)
甲,乙,丙三个同学同时报名参加某重点高校2012年自主招生.高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格.因为甲,乙,丙三人各有优势,甲,乙,丙三人审核过关的概率分别为0.5,0.6,0.4,审核过关后,甲,乙,丙三人文化测试合格的概率分别为0.6,0.5,0.75.
(1)求甲,乙,丙三人中只有一人通过审核的概率;
(2)设甲,乙,丙三人中获得自主招生入选资格的人数为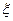 ,求随机变量
,求随机变量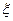 的期望.
的期望.
如图,在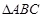 中,
中,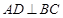 ,垂足为
,垂足为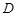 ,且
,且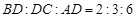 .
.
(Ⅰ)求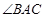 的大小;
的大小;
(Ⅱ)设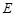 为
为 的中点,已知
的中点,已知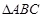 的面积为15,求
的面积为15,求 的长
的长 
(本小题满分14分)在周长为定值的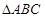 中,已知
中,已知 ,动点
,动点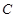 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点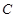 运动时,
运动时,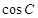 有最小值
有最小值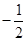 .
.
(1) 以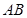 所在直线为
所在直线为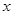 轴,线段
轴,线段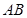 的中垂线为
的中垂线为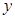 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线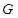 的方程;
的方程;
(2) 过点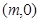 作圆
作圆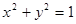 的切线
的切线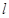 交曲线
交曲线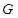 于
于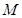 ,
,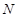 两点.将线段MN的长|MN|表示为
两点.将线段MN的长|MN|表示为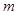 的函数,并求|MN|的最大
的函数,并求|MN|的最大 值.
值.
(本小题满分13分)已知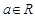 ,函数
,函数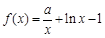 ,
,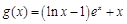 .
.
(1)判断函数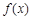 在
在 区间
区间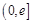 上的单调性(其中
上的单调性(其中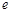 为自然对数的
为自然对数的 底数);
底数);
(2)是否存在实数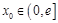 ,使曲线
,使曲线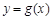 在点
在点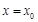 处的切线与
处的切线与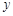 轴垂直
轴垂直
若存在,求出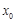 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
本小题满分12分)如图菱形 的边长为
的边长为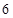 ,
,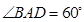 ,
,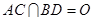 .将菱形
.将菱形 沿对角线
沿对角线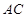 折起,得到三棱锥
折起,得到三棱锥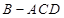 ,
, 点
点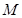 是棱
是棱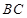 的中点,
的中点,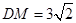 .
.
(1) 求证: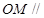 平面
平面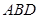 ;
;
(2) 求证:平面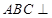 平面
平面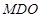 ;
;
(3) 求三棱锥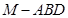 的体积.
的体积.
(本小题满分12分)已知直线 :
: 与直线
与直线 :
: 互相平行,经过点
互相平行,经过点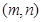 的直线
的直线 与
与 ,
, 垂直,且被
垂直,且被 ,
, 截得的线段长为
截得的线段长为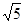 ,试求直线
,试求直线 的方程.
的方程.