(本小题满分12分)已知函数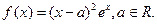
(I)求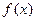 的单调区间;
的单调区间;
(II)若对于任意的 ,都有
,都有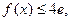 求a的取值范围。
求a的取值范围。
(本小题满分12分)
某班同学利用国庆节进行社会实践,对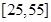 岁的人群随机抽取
岁的人群随机抽取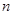 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: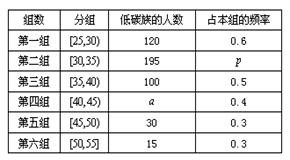

(Ⅰ)补全频率分布直方图并求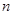 、
、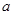 、
、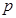 的值;
的值;
(Ⅱ)为调查该地区的年龄与生活习惯是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下列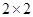 维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?
维列表,并判断能否有99.9%的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关?
参考公式: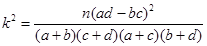
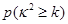 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
是否低碳族 年龄组 年龄组 |
青年 |
老年 |
| 低碳族 |
||
| 非低碳族 |
(本小题满分12分)已知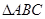 的周长为
的周长为 ,且
,且 .
.
(Ⅰ)求边长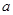 的值;(Ⅱ)若
的值;(Ⅱ)若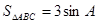 ,求
,求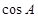 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|x+1|+|x﹣2|﹣m
(I)当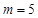 时,求f(x) >0的解集;
时,求f(x) >0的解集;
(II)若关于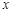 的不等式f(x) ≥2的解集是
的不等式f(x) ≥2的解集是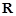 ,求
,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线C1: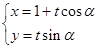 (t为参数),圆C2:
(t为参数),圆C2: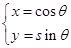 (θ为参数).
(θ为参数).
(I)当α=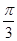 时,求C1与C2的交点的直角坐标;
时,求C1与C2的交点的直角坐标;
(II)过坐标原点O作 C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
C1的垂线,垂足为A,P为OA的中点.当α变化时,求P点轨迹的参数方程,并指出它是什么曲线.
.选修 4-1:几何证明选讲
4-1:几何证明选讲
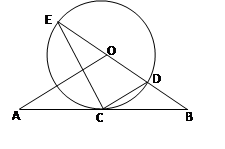
如图,直线 经过⊙
经过⊙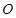 上的点
上的点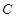 ,并且
,并且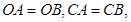 ⊙
⊙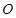 交直
交直 线
线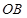 于
于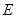 ,
,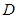 ,连接
,连接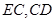 .
.
(I)求证:直线 是⊙
是⊙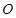 的切线;
的切线;
(II)若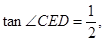 ⊙
⊙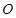 的半径为
的半径为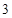 ,求
,求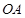 的长.
的长.