设
(1)当 时,求:函数
时,求:函数 的单调区间;
的单调区间;
(2)若 时,求证:当
时,求证:当 时,不等式
时,不等式
已知函数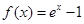
(1)证明:对于一切的实数x都有f(x) x;
x;
(2)若函数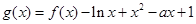 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围
(3)证明:
过抛物线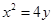 的焦点
的焦点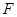 作倾斜角为
作倾斜角为 的直线交抛物线于
的直线交抛物线于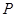 、
、 两点,过点
两点,过点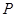 作抛物线的切线
作抛物线的切线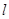 交
交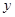 轴于点
轴于点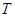 ,过点
,过点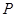 作切线
作切线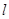 的垂线交
的垂线交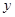 轴于点
轴于点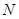 。
。
(1) 若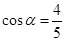 ,求此抛物线与线段
,求此抛物线与线段 以及线段
以及线段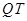 所围成的封闭图形的面积。
所围成的封闭图形的面积。
(2) 求证: ;
;
如图, 是棱长为
是棱长为 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且 .
.
(1)求证: ;
;
(2)当 、
、 、
、 、
、 共面时,求:面
共面时,求:面 与面
与面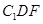 所成二面角的余弦值.
所成二面角的余弦值.
已知函数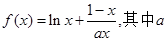 为大于零的常数。
为大于零的常数。
(1)若函数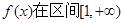 内调递增,求a的取值范围;
内调递增,求a的取值范围;
(2)求函数 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
已知数列{an}满足S n + a n= 2n +1.
(1)写出a1,a2,a3, 并推测a n的表达式;
(2)用数学归纳法证明所得的结论.