（本小题满分10分）某商店根据以往某种新产品的销售记录，绘制了日销售量的频率分布直方图，如图所示.将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.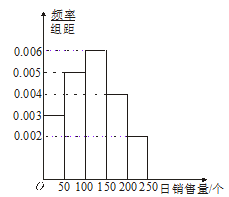
（1）估计日销售量的众数；
（2）求在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率；
（3）用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列.
(本题满分12分)在某次射击比赛中共有5名选手，出场时甲、乙、丙三人不能相邻。求（1）共有多少种不同的出场顺序？
（2）若甲、乙、丙三人每次射击命中目标的概率都为0.6,求三人各射击一次至少有一
人命中目标的概率。
（3）若甲、乙、丙三人每次射击命中目标的概率分别为0.7,0.6,0.5，求三人各射击一
次至少有两人命中目标的概率。
(本题满分13分)在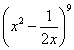
展开式中，求：
（1）第6项；（2） 第3项的系数；（3）常数项。
在10件产品中，有8件合格品，2件次品.从这10件产品中任意抽出3件. 求（Ⅰ）抽出的3件产品中恰好有1件是次品的概率；
（Ⅱ）抽出的3件产品中至少有1件是次品的概率.
证明：
。
在直三棱柱
中，
，直线
与平面
成
角；
（1）求证：平面
平面
；
（2）求二面角
的正弦值.