(本小题满分10分)盒中有大小相同的编号为1,2,3,4,5,6的6只小球,规定:从盒中一次摸出两只球,如果这两只球的编号均能被3整除,则获得一等奖,奖金10元,如果这两只球的编号均为偶数,则获得二等奖,奖金2元,其他情况均不获奖.
(1)若某人参加摸球游戏一次获奖金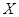 元,求
元,求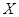 的分布列;
的分布列;
(2)若某人摸一次且获奖,求他获得一等奖的概率.
(本小题满分12分)
已知向量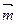 ="(sinA" ,sinB),
="(sinA" ,sinB), =(cosB,cosA),
=(cosB,cosA),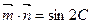 且A、B、C分别为△ABC的三边
且A、B、C分别为△ABC的三边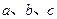 所对的角。
所对的角。
(Ⅰ)求角C的大小;
(Ⅱ)若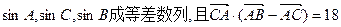 ,求c边的长。
,求c边的长。
(本小题满分12分)
已知 是等差数列,其中
是等差数列,其中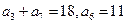 .
.
(Ⅰ)求数列 通项
通项 ;
;
(Ⅱ)若数列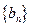 满足
满足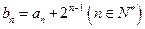 ,求数列
,求数列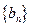 的前
的前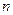 项和
项和 .
.
(本小题满分14分)
设 是椭圆
是椭圆 上的两点,点
上的两点,点 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆交于
的垂直平分线与椭圆交于 两点.
两点.
(Ⅰ)当 时,过点P(0,1)且倾斜角为
时,过点P(0,1)且倾斜角为 的直线与椭圆相交于E、F两点,求
的直线与椭圆相交于E、F两点,求 长;
长;
(Ⅱ)确定 的取值范围,并求直线CD的方程.
的取值范围,并求直线CD的方程.
(本小题满分12分)
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点 (4,
(4, )到焦点的距离为5.
)到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
 .
.
(本小题满分12分)
在锐角 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,且
,且 ,
,
(Ⅰ)求角 ;
;
( Ⅱ)若边
Ⅱ)若边 ,
,  的面积等于
的面积等于 , 求边长
, 求边长 和
和 .
.