如图,在四棱锥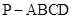 中,底面
中,底面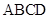 为菱形,
为菱形,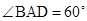 ,
, 为
为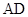 的中点.
的中点.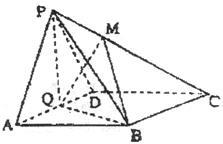
(1)若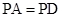 ,求证:平面
,求证:平面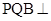 平面
平面 ;
;
(2)设点 是线段
是线段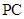 上的一点,
上的一点,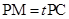 ,且
,且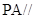 平面
平面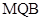 .
.
(1)求实数 的值;
的值;
(2)若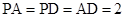 ,且平面
,且平面 平面
平面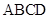 ,求二面角
,求二面角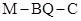 的大小.
的大小.
已知直线l过点P(3,1)且被两平行线l1:x+y+1=0,l2:x+y+6=0截得的线段长为5,求直线l的方程.
求过两直线l1:x+y+1=0,l2:5x-y-1=0的交点,且与直线3x+2y+1=0的夹角为 的直线方程.
的直线方程.
已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0,
(1)试判断l1与l2是否平行;
(2)l1⊥l2时,求a的值.
已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是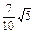 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是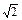 ∶
∶ .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
过点P(3,0)作一直线,使它夹在两直线l1:2x-y-2=0与l2:x+y+3=0之间的线段AB恰被点P平分,求此直线的方程.