已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是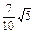 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是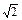 ∶
∶ .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
已知集合A={y|y=x2- x+1,x∈[
x+1,x∈[ ,2]},B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
,2]},B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若( A)∩B=⌀,求m的值.
A)∩B=⌀,求m的值.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.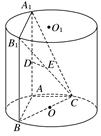
(1)证明:DE∥面ABC;
(2)求四棱锥CABB1A1与圆柱OO1的体积比.
右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
(1)请画出该几何体的三视图;
(2)求四棱锥BCEPD的体积.