如图,在矩形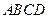 中,
中,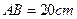 ,
,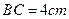 ,点
,点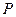 从
从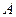 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点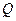 从
从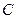 开始沿
开始沿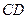 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点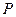 、
、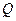 分别从
分别从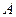 、
、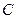 同时出发,当其中一点到达
同时出发,当其中一点到达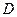 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。
⑴t为何值时,四边形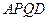 为矩形?
为矩形?
⑵如图10-20,如果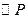 和
和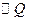 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时,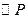 和
和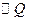 外切。
外切。
请将式子: 化简后,再选择一个合适的
化简后,再选择一个合适的 的值代入求值.
的值代入求值.
(每小题5分,共10分)
(1)计算: ;
;
(2)解方程: .
.
点P为抛物线 (m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图像与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图像与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(1)如图(1)当m=2,点P横坐标为4时,求Q点的坐标;
(2)设点Q(a,b),用含m、b的代数式表示a;
(3)如图(2),点Q在第一象限内,点D在x轴的正半轴上,点C为OD的中点,QO平分∠AQC,AQ=2QC,当QD=m时,求m的值.
如图(a),在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.
(1)点C的坐标是,当点D运动8.5秒时所在位置的坐标是;
(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值时,S最大;
(3)如图(b),另有一点E在线段AB上以同样速度由点A向点B运动,若点E与点D同时出发,问在运动5秒钟内,以点D、A、E为顶点的三角形何时与△OCD相似?(只考虑以点A、O为对应顶点的情况)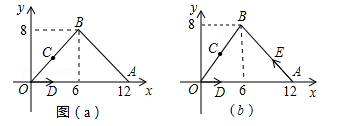
如图①,一条笔直的公路上有A、B、C三地,B.C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图像进行以下探究:
(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图像,求甲车到A地的距离y1与行驶时间x的函数表达式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.