某私营玩具厂招工广告称：“本厂工人工作时间：每天工作8小时，每月工作25天；待遇：熟练工人按计件付工资，多劳多得，且计件工资不少于1000元时，每月另加福利工资100元，按月结算……”． 该厂只生产两种玩具：小狗和小汽车，熟练工人晓凤一月份领工资1145元，她记录了如下一些数据：
(1). 根据表格中的信息，试求出做1个小汽车所需时间和计件工资各是多少?
(2). 设晓凤某月生产小狗x个，小汽车y个，月工资(计件工资+福利工资=月工资)为W元．试求W与x的函数关系式.(不需写出自变量x的取值范围)
8分
(3). 有一天，厂方从销量方面考虑，对生产作了调整：每个工人每月生产小狗的个数不少于生产小汽车个数的2倍，假设晓凤的工作效率不变，且服从厂家安排，请运用数学知识说明厂家招工广告是否有欺诈行为．
0分
如图，已知△OAB的顶点A（﹣6，0），B（0，2），O是坐标原点，将△OAB绕点O按顺时针旋转90°，得到△ODC．
（1）写出C，D两点的坐标；
（2）求过A，D，C三点的抛物线的解析式，并求此抛物线顶点E的坐标；
（3）证明AB⊥BE．
如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．连接OC交AE于点H。
（1）求证：GC⊥OC．
（2）求证：AF=CF．
（3）若∠EAB=30°，CF=2，求GA的长．
已知函数y=mx2－6x＋1（m是常数）．
⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
⑵若该函数的图象与x轴只有一个交点，求m的值．
如图：在△ABC中，AB=2，BC=2
，AC=4，点O是AC的中点；回答下列问题：
（1）∠BAC=°
（2）画出将△ABC绕点O旋转180°得到的△A1DC1(A→A1B→D C→C1），写出四边形ABCD的形状。
（3）尺规作图：在图中作出△ABC的高线AE（保留作图痕迹），并回答在四边形ABCD的边上（点A除外）是否存在点F，使∠EAC=∠EFC; 若存在点F，写出这样的点F一共有几个？并直接写出DF的长。若不存在这样的点F，请简要说明理由。
已知关于x的方程
．
（1）若这个方程有实数根，求k的取值范围；
（2）若这个方程有一个根为1，求k的值；
（3）若以方程的两个根为横坐标、纵坐标的点恰在反比例函数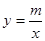
的图象上，求满足条件的m的最小值．