(本题11分)如图,矩形ABCD中,AB=6,BC=2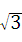 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;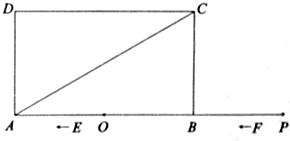
(本小题满分12分)
(理)已知函数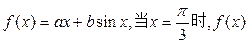 取得极小值
取得极小值 .
.
(Ⅰ)求a,b的值;
(Ⅱ)设直线 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有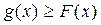 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
试证明:直线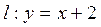 是曲线
是曲线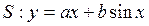 的“上夹线”.
的“上夹线”.
(本小题满分10分)(改编题)
在△ABC中,内角A、B、C的对边分别为a、b、c,已知a、b、c成等比数列,且cosB=.
(1)求cotA+cotC的值;
(2)设·=,求a+c的值.
(本小题满分12分)(原创题)
在平面直角坐标系中,已知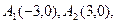
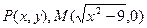 ,若实数
,若实数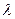 使向量
使向量
 。
。
(1)求点 的轨迹方程,并判断
的轨迹方程,并判断 点的轨迹是怎样的曲线;
点的轨迹是怎样的曲线;
(2)当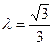 时,过点
时,过点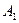 且斜率为
且斜率为 的直线与此时(1)中的曲线相交的另一点为
的直线与此时(1)中的曲线相交的另一点为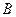 ,能否在直线
,能否在直线 上找一点
上找一点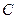 ,使
,使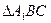 为正三角形(请说明理由)。
为正三角形(请说明理由)。
已知数列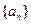 中,
中,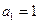 ,
,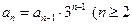 且
且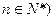
(1)求数列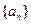 的通项公式;
的通项公式;
(2)设函数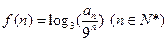 ,数列
,数列 的前
的前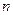 项和为
项和为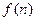 ,求
,求 的通项公式;
的通项公式;
(3)求数列 的前
的前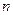 项和
项和 。
。
已知二次函数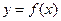 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为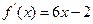 ,数列
,数列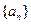 的前n项和为
的前n项和为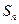 ,点
,点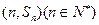 均在函数
均在函数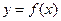 的图像上。
的图像上。
(1)求数列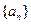 的通项公式;
的通项公式;
(2)设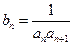 ,
,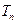 是数列
是数列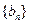 的前n项和,求使得
的前n项和,求使得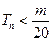 对所有
对所有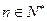 都成立的最小正整数m;
都成立的最小正整数m;