如图①, 已知抛物线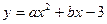 (a≠0)与
(a≠0)与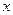 轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式;
轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式;
(2) 设抛物线的对称轴与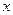 轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
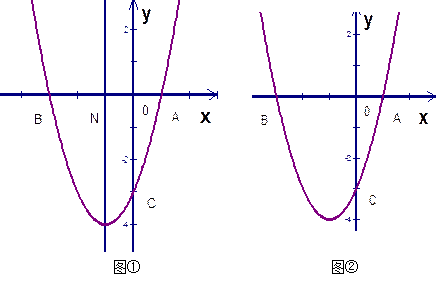
(3) 如图②,若点E为第三象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
 |
如图,已知 的面积为
的面积为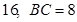 .现将
.现将 沿直线
沿直线 向右平移
向右平移 (
( <8)个单位到
<8)个单位到 的位置.
的位置.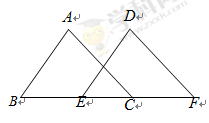
(1)求 的
的 边上的高;
边上的高;
(2)连结 、
、 ,设
,设 .
.
①求线段 的长;
的长;
②当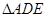 是等腰三角形时,求
是等腰三角形时,求 的值.
的值.
如图,已知△ABC和△ECD都是等腰直角三角形,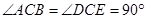 ,
,
点D为AB边上一点.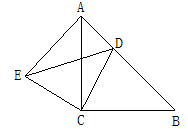
(1)求证:△ACE≌△BCD;
(2)求证:△ADE是直角三角形;
(3)已知△ADE的面积为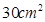 ,
, ,求
,求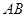 的长.
的长.
某中学对全校学生进行文明礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图.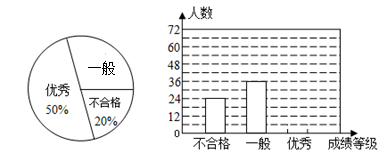
请你根据图中所给的信息解答下列问题:
(1)请将以上条形统计图补充完整;
(2)“一般”等级所在扇形的圆心角的度数是度;
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.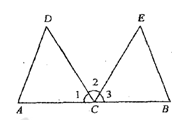
(1)求证:△ACD≌△BCE;
(2)若∠D=47°,求∠B的度数.
符号“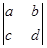 ”称为二阶行列式,规定它的运算法则为:
”称为二阶行列式,规定它的运算法则为: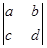
 .
.
(1)计算: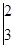
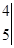 =;(直接写出答案)
=;(直接写出答案)
(2)化简二阶行列式: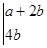
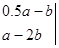 .
.