(本题满分12分)设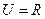 ,
,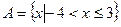 ,
,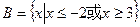 ,求:
,求:
(1)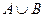 ; (2)
; (2)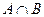 ; (3)
; (3)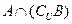
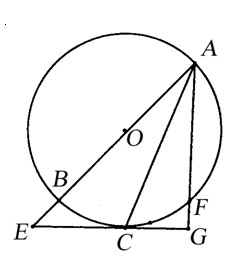
直线AB过圆心O,交圆O于A、B,直线AF交圆O于F
(不与B重合),直线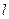 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
求证:(1)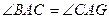
(2)
请用你所学过的数学知识证明“糖水加糖会变甜”(假定糖水始终为不饱和溶液)。
已知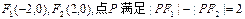 ,记点P的轨迹为E.
,记点P的轨迹为E.
(1)求轨迹E的方程;
(2)设直线l过点F2且与轨迹E交于P、Q两点,若无论直线l绕点F2怎样转动,在x轴上总存在定点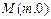 ,使
,使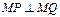 恒成立,求实数m的值.
恒成立,求实数m的值.
已知某椭圆的焦点F1(-4,0),F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同两点A(x 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
求过点 且圆心在直线
且圆心在直线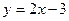 上的圆的方程
上的圆的方程