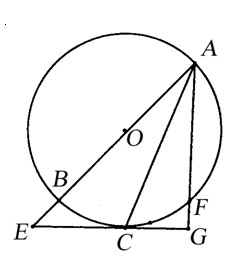
直线AB过圆心O,交圆O于A、B,直线AF交圆O于F
(不与B重合),直线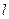 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
求证:(1)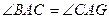
(2)
(1)已知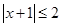 ,
, ,求证:
,求证: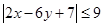 ;
;
(2)已知正数 满足关系
满足关系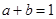 ,求证:
,求证: .
.
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 |
A样式 |
B样式 |
C样式 |
| 10W |
2000 |
z |
3000 |
| 30W |
3000 |
4500 |
5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
已知复数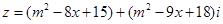 ,实数
,实数 取什么值时,
取什么值时,
(1)复数 是纯虚数?
是纯虚数?
(2)复数 对应的点位于第三象限?
对应的点位于第三象限?
已知函数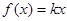 ,
,
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若不等式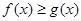 在区间(0,+
在区间(0,+ 上恒成立,求
上恒成立,求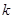 的取值范围;
的取值范围;
(3)求证: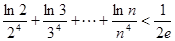
设 ,其中
,其中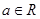 .
.
(1)若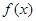 有极值,求
有极值,求 的取值范围;
的取值范围;
(2)若当 ,
,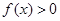 恒成立,求
恒成立,求 的取值范围.
的取值范围.