(本题12分)已知函数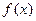 对任意实数p、q都满足
对任意实数p、q都满足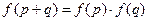
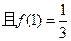 .
.
(Ⅰ)当
 时,求
时,求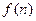 的表达式;
的表达式;
(Ⅱ)设 求
求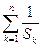 ;
;
(Ⅲ)设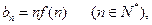 求证:
求证: .
.
(本小题10分). 如图,设椭圆 (a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为
(a>b>0)的右焦点为F(1,0),A为椭圆的上顶点,椭圆上的点到右焦点的最短距离为 -1.过F作椭圆的弦PQ,直线AP,AQ分别交直线
-1.过F作椭圆的弦PQ,直线AP,AQ分别交直线 于点M,N.
于点M,N.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 求当三角形AMN面积最小时直线PQ的方程.
(本小题9分). 如图所示, ⊥平面
⊥平面 ,
, ,
, ,
, 为
为 中点.
中点.
(1)证明: ;
;
(2)若 与平面
与平面 所成角的正切值为
所成角的正切值为 ,求二面角
,求二面角 -
- -
- 的正弦值.
的正弦值.
(本小题8分). 已知圆 :
:  和圆外一点
和圆外一点 (1,
(1,  ),
),
(1)若直线 经过原点
经过原点 ,且圆
,且圆 上恰有三个点到直线
上恰有三个点到直线 的距离为
的距离为 ,求直线
,求直线 的方程;
的方程;
(2)若经过 的直线
的直线 与圆
与圆 相切,切点分别为
相切,切点分别为 ,求切线
,求切线 的方程及
的方程及 两切点所在的直线方程.
两切点所在的直线方程.
(本小题7分).如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ,
, ,
, 是
是 的中点,
的中点, 交
交 于点
于点 .
.
(1)证明 //平面
//平面 ;
;
(2)证明 ⊥平面
⊥平面 ;
;
(3)求 .
.
(本小题6分)已知直线l在两坐标轴上的截距相等,且点 到直线
到直线 的距离为
的距离为 ,求直线
,求直线 的方程.
的方程.