(本小题满分12分)
给定椭圆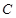 :
: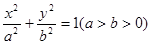 ,称圆心在原点
,称圆心在原点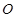 ,半径为
,半径为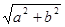 的圆是
的圆是
椭圆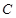 的“准圆”。若椭圆
的“准圆”。若椭圆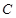 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到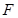 的距
的距
离为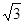 .
.
(Ⅰ)求椭圆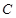 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点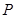 是椭圆
是椭圆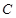 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点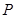 作直线
作直线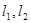 使得
使得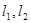 与椭
与椭
圆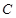 都只有一个交点,且
都只有一个交点,且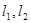 分别交其“准圆”于点
分别交其“准圆”于点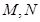 ;
;
(1)当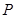 为“准圆”与
为“准圆”与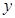 轴正半轴的交点时,求
轴正半轴的交点时,求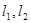 的方程.
的方程.
(2)求证: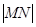 为定值.
为定值.
(本小题满分15分)已知函数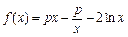 .
.
(I)若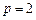 ,求曲线
,求曲线 在点
在点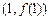 处的切线方程;
处的切线方程;
若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数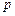 的取值范围;
的取值范围;
(III)设函数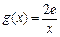 ,若在
,若在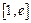 上至少存在一点
上至少存在一点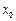 ,使得
,使得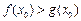 成立,求实数
成立,求实数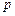 的取值范围.
的取值范围.
(本小题满分15分)已知O为坐标原点,点A、B分别在x轴,y轴上运动,且|AB|=8,动点P满足 =
=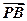 ,设点P的轨迹为曲线C,定点为M(4
,设点P的轨迹为曲线C,定点为M(4 ,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面
,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面 积的
积的 最大值.
最大值.
(本小题 满分14分)已知定义域为R的函数
满分14分)已知定义域为R的函数 是奇函
是奇函 数.
数.
(1)求a的值;(2)判断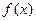 的单调性(不需要写出理由);
的单调性(不需要写出理由);
(3)若对任意的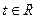 ,不等式
,不等式 恒成立,求
恒成立,求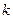 的取值范围.
的取值范围.
(本小题满分14分)(I)已知函数 的最小正周期;(II)设
的最小正周期;(II)设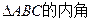 A、B、C的对边分别为a、b、c,且
A、B、C的对边分别为a、b、c,且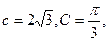 若向量
若向量 的值。
的值。
已知集合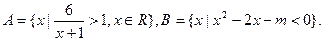
(1)当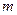 =3时,求
=3时,求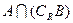 ;
;
(2)若 ,求实数
,求实数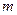 的值.
的值.