在△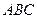 中,内角
中,内角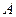 ,
,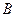 ,
, 对边的边长分别是
对边的边长分别是 ,已知
,已知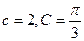 .
.
(1)若△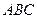 的面积等于
的面积等于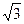 ,求
,求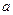 ,
,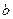 ;
;
(2)若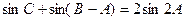 ,求△
,求△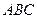 的面积.
的面积.
函数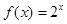 和
和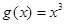 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
(1)请指出示意图中曲线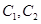 分别对应哪一个函数?
分别对应哪一个函数?
(2) ,且
,且 ,指出
,指出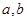 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,请把
四个数按从小到大的顺序排列.
已知集合 ,
,
(1)求 ;
;
(2)若集合 ,满足
,满足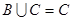 ,求实数
,求实数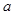 的取值范围.
的取值范围.
函数 ;
;
(1)若 在
在 处取极值,求
处取极值,求 的值;
的值;
(2)设直线 和
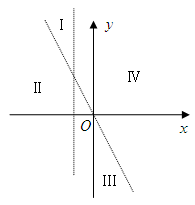
和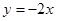 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若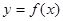 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的 的范围.
的范围.
已知函数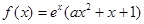 ,
, ;
;
(1)讨论 的单调性;
的单调性;
(2)若 在
在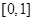 上的最大值为
上的最大值为 ,求
,求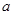 的值.
的值.
以原点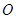 为极点,以
为极点,以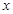 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ,过点
,过点 的直线
的直线 的参数方程为
的参数方程为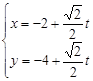 ,设直线
,设直线 与曲线
与曲线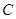 分别交于
分别交于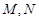 ;
;
(1)写出曲线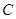 和直线
和直线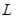 的普通方程;
的普通方程;
(2)若 成等比数列,求
成等比数列,求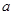 的值.
的值.