(12分)已知直线l与点A(3,3),B(5,2)的距离相等,且过两直线l1:3x-y-1=0与l2:x+y-3=0的交点,求直线l的方程.
(本小题满分12分)
函数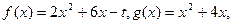 其中t为常数.
其中t为常数.
(1)若对任意的 ,都有
,都有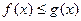 成立,求t的取值范围;
成立,求t的取值范围;
(2)若对任意的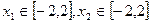 ,都有
,都有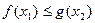 成立,求t的取值范围.
成立,求t的取值范围.
(本小题满分12分)
已知条件p: 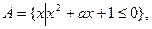 条件q:
条件q:  若
若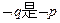 的充分但不必要条件,求实数
的充分但不必要条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)
本地一公司计划2011年在省、市两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,省、市电视台的广告收费标准分别为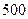 元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?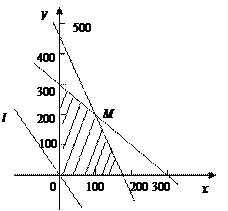
(本小题满分12分)
已知向量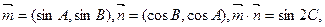 且A、B、C分别为△ABC的三边a、b、c所对的角.
且A、B、C分别为△ABC的三边a、b、c所对的角.
(1)求角C的大小;
(2)若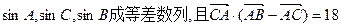 ,求c边的长.
,求c边的长.
(本小题满分12分)
已知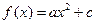 的图象经过点
的图象经过点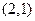 ,且在
,且在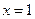 处的切线方程是
处的切线方程是
(1)求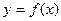 的解析式;
的解析式;
(2)点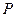 是直线
是直线 上的动点,自点
上的动点,自点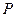 作函数
作函数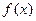 的图象的两条切线
的图象的两条切线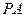 、
、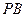
(点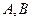 为切点),求证直线
为切点),求证直线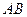 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。