假设关于某市房屋面积
（平方米）与购房费用
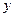(万元),有如下的统计数据：
| x(平方米) |
80 |
90 |
100 |
110 |
| y(万元) |
42 |
46 |
53 |
59 |
由资料表明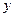对呈线性相关。
（1）求回归直线方程;
（2）若在该市购买120平方米的房屋,估计购房费用是多少?
公式: 
已知函数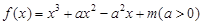
．
若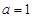
时函数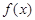
有三个互不相同的零点，求实数
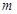的取值范围；
若对任意的
，不等式
对任意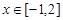
恒成立，求实数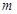的取值范围．
已知椭圆C的中心在原点，焦点在坐标轴上，短轴的一个端点B（0，4），离心率e=0．6．
（1）求椭圆C的方程；
（2）若O（0，0），P（2，2），试探究在椭圆C内部是否存在整点Q（平面内横、纵坐标都是
整数的点为整点），使得△OPQ的面积S△OPQ=4?若存在，请指出共有几个这样的点（不必具体求出这些点的坐标）；否则，说明理由．
已知等比数列{
}的前
项和为
，且满足
．
（1）求
的值及数列{}的通项公式；
（2）若数列{
}满足
,求数列{}的前和
．
已知
图象过点
，且在
处的切线方程是
．
（1）求
的解析式；
（2）求在区间
上的最大值和最小值．
已知
，函数
．
（1）求函数
的最小正周期；
（2）已知
，且
，求
的值．