已知 图象过点
图象过点 ,且在
,且在 处的切线方程是
处的切线方程是 .
.
(1)求 的解析式;
的解析式;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
如图,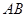 为圆
为圆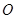 的直径,点
的直径,点 .
. 在圆
在圆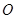 上,且
上,且 ,矩形
,矩形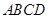 所在的平面和圆
所在的平面和圆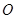 所在的平面互相垂直,且
所在的平面互相垂直,且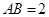 ,
,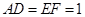 .
.
(1)设 的中点为
的中点为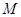 ,求证:
,求证: 平面
平面 ;
;
(2)求四棱锥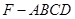 的体积.
的体积.
已知命题 :方程
:方程 所表示的曲线为焦点在
所表示的曲线为焦点在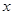 轴上的椭圆;命题
轴上的椭圆;命题 :实数
:实数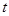 满足不等式
满足不等式 .
.
(1)若命题 为真,求实数的取值范围;
为真,求实数的取值范围;
(2)若命题 是命题
是命题 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知函数 为奇函数.
为奇函数.
(1)若 ,求函数
,求函数 的解析式;
的解析式;
(2)当 时,不等式
时,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的最小值;
的最小值;
(3)当 时,求证:函数
时,求证:函数 在
在 上至多有一个零点.
上至多有一个零点.
某种产品特约经销商根据以往当地的需求情况,得出如下该种产品日需求量的频率分布直方图.
(1)求图中 的值,并估计日需求量的众数;
的值,并估计日需求量的众数;
(2)某日,经销商购进130件该种产品,根据近期市场行情,当天每售出 件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为
件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为 件(
件( ),纯利润为
),纯利润为 元.
元.
(ⅰ)将 表示为
表示为 的函数;
的函数;
(ⅱ)根据直方图估计当天纯利润 不少于
不少于 元的概率.
元的概率.
已知函数 ,
, .
.
(1)若函数 在
在 上不具有单调性,求实数
上不具有单调性,求实数 的取值范围;
的取值范围;
(2)若 .
.
(ⅰ)求实数 的值;
的值;
(ⅱ)设 ,
, ,
, ,当
,当 时,试比较
时,试比较 ,
, ,
, 的大小.
的大小.