(本题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
(Ⅰ)甲喝两瓶 饮料,均合格的概率
饮料,均合格的概率
(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
如图,在正方体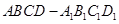 中,
中, 是
是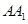 的中点.
的中点.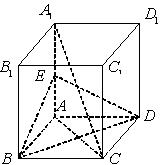
(1)求证: 平面
平面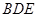 ;
;
(2)求证:平面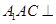 平面
平面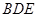 .
.
已知命题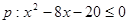 ,命题
,命题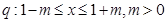 ,若
,若 是
是 的必要不充分条件,求实数m的取值范围。
的必要不充分条件,求实数m的取值范围。
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于 轴(垂足为T),与抛物线交于不同的两点P、Q,且
轴(垂足为T),与抛物线交于不同的两点P、Q,且 .
.
(Ⅰ)求点T的横坐标 ;
;
(Ⅱ)若椭圆C以F1,F2为焦点,且F1,F2及椭圆短轴的一个端点围成的三角形面积为1.
① 求椭圆C的标准方程;
② 过点F2作直线l与椭圆C交于A,B两点,设 ,若
,若 的取值范围.
的取值范围.
已知函数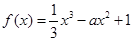
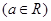 .
.
(Ⅰ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅱ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
如图(1),在等腰梯形CDEF中,CB、DA是梯形的高,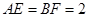 ,
,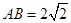 ,现将梯形沿CB、DA折起,使EF//AB且
,现将梯形沿CB、DA折起,使EF//AB且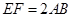 ,得一简单组合体
,得一简单组合体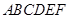 如图(2)所示,已知
如图(2)所示,已知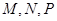 分别为
分别为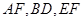 的中点.
的中点.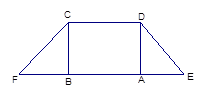
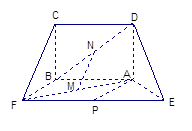
图(1) 图(2)
(Ⅰ)求证: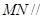 平面
平面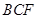 ;
;
(Ⅱ)求证: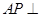 平面
平面 .
.