(本小题满分12分)
某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽9米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值.
|
(本小题满分12分)已知函数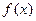 满足
满足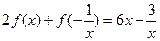 ,对任意
,对任意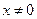 恒成立,在数列
恒成立,在数列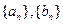 中,
中, 对任意
对任意
(1)求函数的解析式
(2)求数列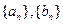 的通项公式
的通项公式
(3)若对任意的实数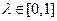 ,总存在自然数k,当
,总存在自然数k,当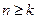 时,
时,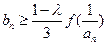 恒成立,求k的最小值。
恒成立,求k的最小值。
(本小题满分12分)
在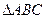 中,角
中,角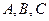 所对的边分别为
所对的边分别为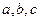 ,满足
,满足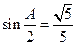 ,且
,且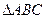 的面积为
的面积为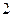 .
.
(1)求 的值
的值
(2)若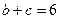 ,求
,求 的值.
的值.
(本小题满分12分)
已知向量 ,求
,求
(1)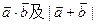 ;
;
(2)若
 的最小值是
的最小值是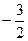 ,求实数
,求实数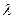 的值.
的值.
(本小题满分12分)
设函数 的定义域为A,不等式
的定义域为A,不等式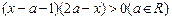 的解集为B.
的解集为B.
(1)求A;
(2)若B A,求实数a的取值范围.
A,求实数a的取值范围.