已知椭圆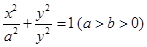 上的点
上的点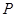 到左、右两焦点
到左、右两焦点 的距离之和为
的距离之和为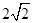 ,离心率为
,离心率为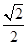 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点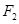 的直线
的直线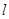 交椭圆于
交椭圆于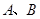 两点.
两点.
(1)若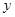 轴上一点
轴上一点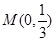 满足
满足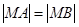 ,求直线
,求直线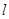 斜率
斜率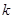 的值;
的值;
(2)是否存在这样的直线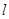 ,使
,使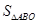 的最大值为
的最大值为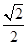 (其中
(其中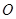 为坐标原点)?若存在,求直线
为坐标原点)?若存在,求直线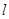 方程;若不存在,说明理由.
方程;若不存在,说明理由.
已知双曲线 的中心在原点,焦点在坐标轴上,离心率
的中心在原点,焦点在坐标轴上,离心率 ,且双曲线过点
,且双曲线过点 ,求双曲线
,求双曲线 的方程.
的方程.
已知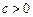 且
且 ,设命题
,设命题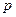 :函数
:函数 在R上单调递减,命题
在R上单调递减,命题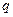 :不等式
:不等式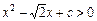 的解集为R,如果命题“
的解集为R,如果命题“ ”为真命题,“
”为真命题,“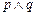 ”为假命题,求实数
”为假命题,求实数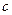 的取值范围
的取值范围
某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了 5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需准备不同的素菜品种多少种?
6女,4男中随机选出3位参加测验.每位女同学能通过测验的概率为0.8,每位男同学能通过测验的概率为0.6.试求:
⑴选出的3位同学中,至少有一位男同学的概率;
⑵10位同学中的女同学甲和男同学乙同时被先选中且通过测验的概率.
如果a(1-a)4+a2(1+2a)k+a3(1+3a)2的展开式中含a4项的系数为114,求正整数k的值。