已知函数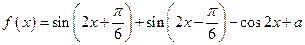 (
(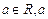 为常数).
为常数).
(1)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)若函数 的图像向左平移
的图像向左平移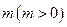 个单位后,得到函数
个单位后,得到函数 的图像关于
的图像关于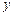 轴对称,求实数
轴对称,求实数 的最小值
的最小值
(本小题满分14分)如图,在一个由矩形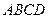 与正三角形
与正三角形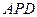 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形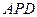 沿
沿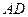 折成四棱锥
折成四棱锥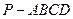 ,使
,使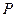 在平面
在平面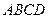 内的射影恰好在边
内的射影恰好在边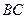 上.
上.

(1)求证:平面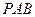 ⊥平面
⊥平面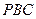 ;
;
(2)求直线 与平面
与平面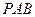 所成角的正弦值.
所成角的正弦值.
|
已知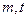 是实数,
是实数, 是抛物线
是抛物线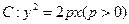 的焦点,直线
的焦点,直线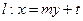 .
.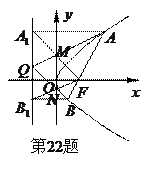 (1)若
(1)若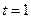 ,且
,且 在直线
在直线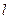 上,求抛物线
上,求抛物线 的方程;
的方程;
(2)当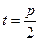 时,设直线
时,设直线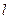 与抛物线
与抛物线 交于
交于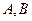 两点,过
两点,过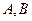 分别作抛物线
分别作抛物线 的准线的垂线,垂足为
的准线的垂线,垂足为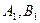 ,连
,连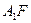 交
交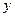 轴于点
轴于点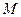 ,连结
,连结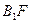 交
交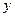 轴于点
轴于点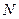 .
.
①证明: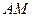 ⊥
⊥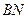 ;
;
②若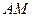 与
与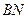 交于点
交于点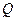 ,记△
,记△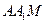 、四边形
、四边形 、△
、△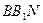 的面积分别为
的面积分别为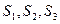 ,问
,问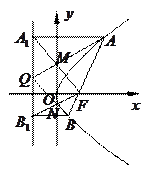 是否存在实数
是否存在实数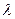 ,使
,使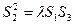 成立?若存在,求出
成立?若存在,求出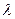 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在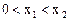 , 使得不等式
, 使得不等式 成立. 若
成立. 若 ,
, 是数列
是数列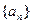 的前
的前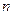 项和.
项和.
(I)求数列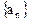 的通项公式;
的通项公式;
(II)设各项均不为零的数列 中,所有满足
中,所有满足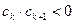 的正整数
的正整数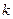 的个数称为这个数列
的个数称为这个数列 的变号数,令
的变号数,令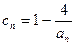 (n为正整数),求数列
(n为正整数),求数列 的变号数;
的变号数;
(Ⅲ)设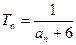 (
(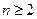 且
且 ),使不等式
),使不等式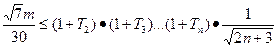 恒成立,求正整数
恒成立,求正整数 的最大值
的最大值
已知椭圆C: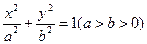 的左焦点为
的左焦点为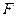 (-1,0),离心率为
(-1,0),离心率为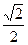 ,过点
,过点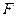 的直线
的直线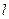 与椭圆C交于
与椭圆C交于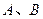 两点.
两点.
(Ⅰ)求椭圆C的方程;
(II)设过点F不与坐标轴垂直的直线交椭圆C于A、 B两点,线段AB的垂直平分线与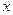 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围.
设函数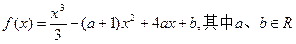
(Ⅰ)若函数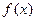 在
在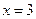 处取得极小值是
处取得极小值是 ,求
,求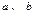 的值;
的值;
(Ⅱ)求函数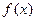 的单调递增区间;
的单调递增区间;
(Ⅲ)若函数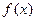 在
在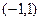 上有且只有一个极值点, 求实数
上有且只有一个极值点, 求实数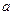 的取值范围.
的取值范围.