(本小题满分12分)
已知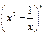 展开式中的二项式系数的和比
展开式中的二项式系数的和比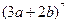 展开式的二项式系数的和大
展开式的二项式系数的和大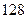 ,求
,求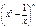 展开式中的系数最大的项和系数最小的项.
展开式中的系数最大的项和系数最小的项.
已知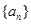 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且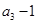 是
是 和
和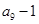 的等比中项,求:
的等比中项,求:
(1)数列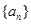 的通项公式;
的通项公式;
(2)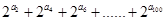 .
.
已知 ,
,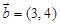 ,
,
(1)若 与
与 垂直,求
垂直,求 的值;
的值;
(2)若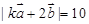 ,求
,求 的值.
的值.
已知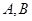 为椭圆
为椭圆 上两动点,
上两动点,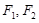 分别为其左右焦点,直线
分别为其左右焦点,直线 过点
过点 ,且不垂直于
,且不垂直于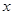 轴,
轴, 的周长为
的周长为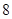 ,且椭圆的短轴长为
,且椭圆的短轴长为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点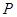 为椭圆
为椭圆 的左端点,连接
的左端点,连接 并延长交直线
并延长交直线 于点
于点 .求证:直线
.求证:直线 过定点.
过定点.
已知函数 .
.
(1)若函数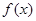 在
在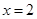 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(2)若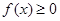 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某分公司经销某种品牌产品,每件产品的成本为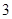 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交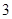 元的管理费,预计当每件产品的售价为
元的管理费,预计当每件产品的售价为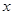 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件.
(1)求该分公司一年的利润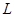 (万元)与每件产品的售价
(万元)与每件产品的售价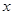 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,该分公司一年的利润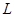 最大?并求出
最大?并求出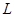 的最大值.
的最大值.