(文)以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y=17时的概率。
(注:方差 ,其中
,其中 为
为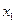 ,
, ,……
,……  的
的
平均数)
(本小题满分12分)已知向量
 。
。
(1)若f(x)=1,求cos(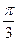 +x)的值;
+x)的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,
求函数f(A)的取值范围。
(本小题满分10分)某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40, 50),[50, 60),…,[90, 100] 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(I)求分数在 [70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ) 根据频率分布直方图估计这次高一年级期中考试的学生成绩的中位数(保留整数)。
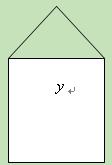
某单位欲用木料制作如下图所示的框架,框架的下部是边长分别为 (单位为:
(单位为: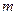 )的矩形,上部是等腰直角三角形,要求框架围成的总面积为
)的矩形,上部是等腰直角三角形,要求框架围成的总面积为 ,问:
,问: 分别是多少(精确到
分别是多少(精确到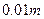 )时用料最省?
)时用料最省?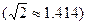
已知 的周长为
的周长为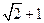 ,且
,且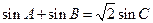 。
。
(1)求边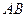 的长;
的长;
(2)若 的面积为
的面积为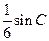 ,求角
,求角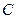 的度数。
的度数。
已知数列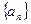 中,
中, =2,
=2,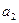 =3,其前
=3,其前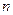 项和
项和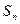 满足
满足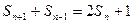
( ,
, 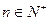 )。
)。
(1)求证:数列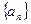 为等差数列,并求
为等差数列,并求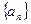 的通项公式;
的通项公式;
(2)设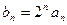 ,求数列
,求数列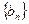 的前
的前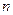 项和
项和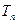 ;
;