（本小题满分10分）某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段[40, 50)，[50, 60)，…，[90, 100] 后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：
（I）求分数在 [70，80)内的频率，并补全这个频率分布直方图；
（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
(Ⅲ) 根据频率分布直方图估计这次高一年级期中考试的学生成绩的中位数(保留整数)。
动直线y =a，与抛物线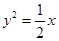
相交于A点，动点B的坐标是
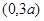，求线段AB中点M的轨迹的方程．
已知点H（-3，0），点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足
.
⑴ 当点P在y轴上移动时，求点M的轨迹G；
⑵ 过点T（-1，0）作直线l与轨迹G交于A、B两点，若在x轴上存在一点E（x0，0），
使得
ABE是等边三角形，求x0的值．
如图所示的多面体是由底面为
的长方体被截面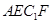
所截面而得到的，其中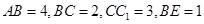
（Ⅰ）求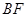
的长；
（Ⅱ）求点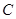
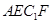到平面的距离
（本小题满分14分）
已知函数
.
(Ⅰ)若曲线
在
和
处的切线互相平行，求
的值；
(Ⅱ)求
的单调区间；
(Ⅲ)设
，若对任意
，均存在
，使得
，求的取值范围.
（本小题满分13分）已知椭圆
的离心率为
，以原点为圆心，椭圆短半轴长为半径的圆与直线
相切，
分别是椭圆的左右两个顶点， 
为椭圆
上的动点.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若与均不重合，设直线
与
的斜率分别为
，证明：
为定值；
（Ⅲ）
为过且垂直于
轴的直线上的点，若
，求点的轨迹方程，并说明轨迹是什么曲线．