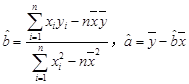一条光线从点P(6,4)射出,与x轴相较于点Q(2,0),经x轴反射,求入射光线和反射光线所在的直线方程。
(本小题满分12分)
已知等差数列{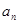 }的公差
}的公差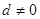 ,
,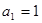 ,且
,且 ,
,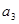 ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列{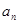 }的公差
}的公差 及通项
及通项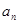 ;
;
(Ⅱ)求数列 的前
的前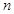 项和
项和
(本小题满分10分)
在△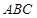 中,角
中,角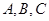 所对的边分别为
所对的边分别为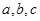 ,已知
,已知 ,
,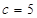 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求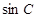 的值.
的值.
已知函数 ,
,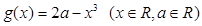
(1)求函数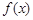 的单调区间;
的单调区间;
(2)求函数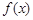 的极值;
的极值;
(3)若任意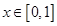 ,不等式
,不等式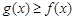 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题14分)已知函数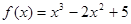
(1)求函数 的极值;
的极值;
(2)求函数 在区间
在区间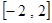 上的最大值和最小值.
上的最大值和最小值.
某镇预测2010年到2014年中心城区人口总数与年份的关系如下表:
| 年份201x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数y(万) |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出线性回归方程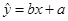 .
.
(3)据此估计2020年该镇人口总数。
参考公式: