（本小题13分）已知函数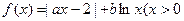
，实数a，b为常数），
（Ⅰ）若a＝1，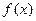
在（0，＋∞）上是单调增函数，求b的取值范围；
（Ⅱ）若a≥2，b＝1，判断方程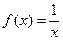
在（0，1]上解的个数。
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsinA=3csinB,a=3,cosB=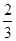
.
(1)求b的值;
(2)求sin（2B-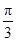
）的值.
在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin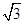B=
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积.
在△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos =2B=1.
(1)求证:a,b,c成等差数列;
(2)若C=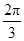
,求
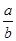的值.
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
,点M在线段PQ上.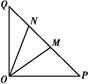
(1)若OM=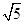
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
已知a,b,c分别为△ABC三个内角A,B,C的对边,c=
asinC-ccosA.
(1)求A;
(2)若a=2,△ABC的面积为,求b,c.