若△ABC和△ADE均为等边三角形，M、N分别是BE、CD的中点．
(1)当△ADE绕A点旋转到如图
①的位置时，求证：CD=BE，△AMN是等边三角形；
(2) 如图②，当∠EAB=30°，AB＝12，AD=
时，求AM的长．
 |
 |
||
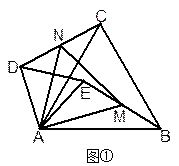如图，直线y=
x+6与x轴交于点B，与y 轴交于点A．以AB为边画正方形ABCD．
（1）求△AOB的面积；
（2）求点C的坐标；
（3）已知点Q（-4，0），点P从点Q出发，以每秒2个单位的速度沿x轴的正方向运动，设运动时间为t秒，当t为何值时，△PBC是等腰三角形．
甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲、y乙与x之间的函数图像如图所示，结合图像解答下列问题：
（1）A、B两地相距km；
（2）求乙车与甲车相遇后，y乙与x之间的函数表达式；
（3）甲、乙两辆汽车出发多长时间两车相距50km．
为了了解我校九年级中考体育测试项目男女长跑（男1000米，女800米）的冬训成绩，组织体育组的老师从九年级十四个班级中随机抽取了部分学生进行测试（满分为8分），并根据测试收集的数据绘制了如下两幅不完整的统计图．根据上述信息，解答下列问题：
（1）本次随机抽取的学生人数为 人；
（2）将条形统计图补充完整，并求出扇形统计图中成绩为6分所对应的扇形的圆心角的度数；
（3）若我校九年级共有800名学生，估计九年级学生长跑成绩不低于7分的人数．
如图，已知□ABCD的对角线AC、BD相交于点O，四边形OCED为菱形．
（1）求证：□ABCD是矩形；
（2）连接AE、BE，AE与BE相等吗？请说明理由．
已知
与
成正比例，当
=-1时，=4，
（1）求出与的函数表达式；
（2）设点（
，-2）在这个函数的图像上，求的值．