如图,在平面直角坐标系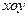 中,抛物线
中,抛物线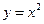 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线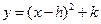 .所得抛物线与
.所得抛物线与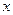 轴交于
轴交于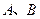 两点(点
两点(点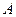 在点
在点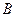 的左边),与
的左边),与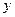 轴交于点
轴交于点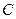 ,顶点为
,顶点为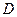 .
.
(1)求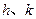 的值;
的值;
(2)求直线AC的函数解析式。
(3)在线段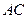 上是否存在点
上是否存在点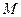 ,使
,使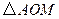 与
与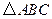 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.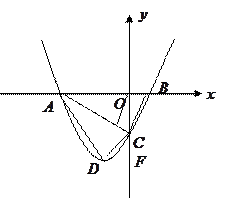
如图是某学校的平面示意图,在8×8的正方形网格中,如果实验楼所在位置的坐标为(-2,-3).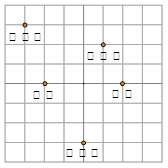
(1)请画出符合题意的平面直角坐标系;
(2)在(1)的平面直角坐标系内表示下列位置:旗杆;校门;图书馆;教学楼.
解不等式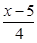 >
>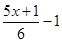 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
探索规律:将连续的偶2,4,6,8,…,排成如下表: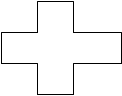 2 4 6 8 10
2 4 6 8 10
12 14 16 18 20
22 24 26 28 30
32 34 36 38 40
……
(1)十字框中的五个数的和与中间的数和16有什么关系?
(2)设中间的数为x ,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2010吗?如能,写出这五位数,如不能,说明理由。
某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-14,+4,-2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
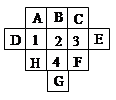
.如图所示,用1、2、3、4标出的四块正方形,以及由字母标出的八块正方形中任意一块,一共要用5块连在一起的正方形折成一个无盖方盒,共有几种不同的方法?请选择合适的方法。