如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴子点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1)设点P的纵坐标为p,写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于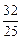 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。
如图,∠l+∠3=180°,∠2+∠D=90°,BE⊥FD,垂足为M,试证明:AB∥CD.
已知:如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠DOE = 4:1.求∠AOF的度数.
判断下列两个命题是否为真命题,若是真命题,给予证明;若是假命题,请举出一个反例。
(1)同旁内角相等,则两直线平行
(2)邻补角的平分线互相垂直.
如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:
因为EF∥AD,所以∠2=()
又因为∠1=∠2,所以∠1=∠3
所以AB∥()
所以∠BAC+=180°()
因为∠BAC=70°,所以∠AGD=.
阅读理解:对于任意正实数a、b,∵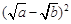 ≥0,∴
≥0,∴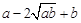 ≥0,
≥0,
∴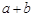 ≥
≥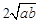 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在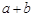 ≥
≥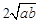 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥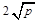 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值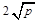 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为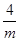 ,考虑何时时周长
,考虑何时时周长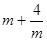 最小。
最小。
∵m>0,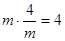 (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m=时,镜框周长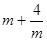 有最小值是;
有最小值是;
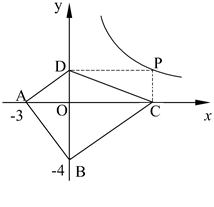
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线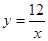 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.