阅读理解:对于任意正实数a、b,∵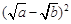 ≥0,∴
≥0,∴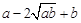 ≥0,
≥0,
∴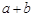 ≥
≥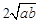 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在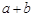 ≥
≥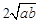 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥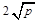 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值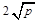 .
.
(1)根据上述内容,回答下列问题:现要制作一个长方形(或正方形),使镜框四周围成的面积为4,请设计出一种方案,使镜框的周长最小。
设镜框的一边长为m(m>0),另一边的为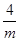 ,考虑何时时周长
,考虑何时时周长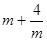 最小。
最小。
∵m>0,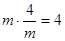 (定值),由以上结论可得:
(定值),由以上结论可得:
只有当m= 时,镜框周长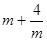 有最小值是 ;
有最小值是 ;
(2)探索应用:如图,已知A(-3,0),B(0,-4),P为双曲线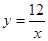 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时△OAB与△OCD的关系.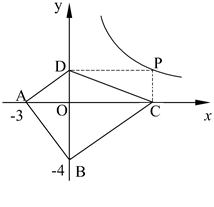
如图,在平面直角坐标系中,直线AB与x轴、y轴的正半轴分别交于点A,B,直线CD与x轴正半轴、y轴负半轴分别交于点D,C,AB与CD相交于点E,点A,B,C,D的坐标分别为(8,0)、(0,6)、(0,﹣3)、(4,0),点M是OB的中点,点P在直线AB上,过点P作PQ∥y轴,交直线CD于点Q,设点P的横坐标为m.
(1)求直线AB,CD对应的函数关系式;
(2)用含m的代数式表示PQ的长;
(3)若以点M,O,P,Q为顶点的四边形是矩形,请直接写出相应的m的值.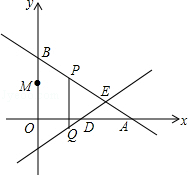
如图,点E,F分别在正方形ABCD的边DA,DC延长线上,且AE﹣CF,连接BE,BF,过点E作EG∥BF,过点F作FG∥BE,EG,FG交于点G.
(1)求证:△ABE≌△CBF;
(2)求证:四边形BEGF是菱形;
(3)若AD=3AE=3,求四边形BEGF的周长.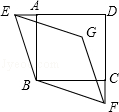
一个容器中有一个进水管和两个出水管,从某一时刻开始2min内只进水不出水,在随后的4min内开启了一个出水管,既进水又出水,每个出水管每分钟出水7.5L,每分钟的进水量和出水量保持不变,容器内的水量y(L)与时间x(min)之间的函数关系如图所示.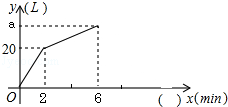
(1)求a的值;
(2)当2≤x≤6时,求y关于x的函数关系式;
(3)若在6min之后,两个出水管均开启,进水管关闭,请在图中补全函数图象.
某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:
(1)在频数分布表中,a的值是 ,b的值是 ;并将频数分布直方图补充完整;
(2)这些学生视力的中位数落在频数分布表中的哪个范围内;
(3)若该校七年级共有800名学生,估计该校七年级学生中视力在4.9以上(包括4.9)的学生有多少名?
七年级部分学生视力的频数分布表
视力 频数(人) 频率
4.0≤x<4.3 10 0.1
4.3≤x<4.6 20 0.2
4.6≤x<4.9 35 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 5 b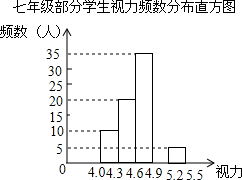
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE是△ABC的中线,∠BCD=22.5°.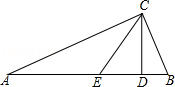
(1)求∠CED的度数;
(2)若CD=1,求△ABC的面积.