如图甲,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图乙),直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2.求y与x之间的函数关系式.
先化简,再求值:(2a– b)2 – 2a(a– b) – (2a2+b2),其中a=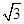 +1,b=
+1,b=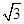 – 1.
– 1.
如图甲,已知⊿ABC和⊿DEF中,∠B=∠DEF,AB=DE,BE="CF." 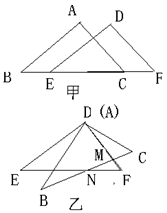
①请说明∠A=∠D的理由;
②⊿ABC可以经过图形的变换得到⊿DEF,请你描述由⊿ABC到⊿DEF的变换过程.
③若图形经过变换后变成图乙,且∠E=370,∠EDB=250,
∠C=580,求∠NMF的度数.
古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两个工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲: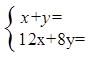 乙:
乙: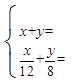
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示____________________,y表示 __________________;
乙:x表示 ____________________,y表示 __________________;
(2)求A、B两工程队分别整治河道多少米?(写出完整的解答过程)
在一个不透明的袋子中装有3个除颜色外完全相同的小球,其中白球1个,黄球1个,红球1个,摸出一个球记下颜色后放回,再摸出一个球,请用列表或树形图法求两次都摸到红球的概率.
先化简,再求值:(2x+5)(x+1)-(x-3)(x+1),其中x=-7