(本题满分9分)如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(1)求此抛物线的解析式及顶点D的坐标;
(2)问点P在何处时,线段PQ最长,最长为多少?
(3)设E为线段OC上的三等分点,连接EP,EQ,若EP=EQ,求点P的坐标.
 |
如图所示,点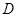 在
在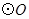 的直径
的直径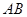 的延长线上,点
的延长线上,点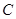 在
在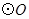 上,且
上,且 ,∠
,∠ °﹒
°﹒
(1)求证: 是
是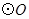 的切线;
的切线;
(2)若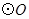 的半径为2,求图中阴影部分的面积﹒
的半径为2,求图中阴影部分的面积﹒
先化简再求值: ,其中x是方程
,其中x是方程 的根﹒
的根﹒
(本题满分12分,每小题6分)
(1)计算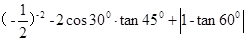
(2)解方程:
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x |
…… |
-2 |
-1 |
0 |
1 |
2 |
…… |
| y |
…… |
0 |
4 |
6 |
6 |
4 |
…… |
从上表可知,下列说法中正确的是________(填写序号)
①抛物线与x轴的一个交点为(3,0) ②函数y=ax2+bx+c的最大值为6
③抛物线的对称轴是直线x= ④在对称轴左侧,y随x增大而增大
④在对称轴左侧,y随x增大而增大
某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入。下表是某周的生产情况(超产记为正、减产记为负):(本题共7分)
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
(1)根据记录的数据可知该厂星期四生产自行车辆;
(2)根据记录的数据可知该厂本周实际生产自行车辆;
(3)产量最多的一天比产量最少的一天多生产自行车辆;
(4)该厂实行每周计件工资制,每生产一辆车可得 60 元,若超额完成任务,则超过部分每辆另奖 15 元;少生产一辆扣 20 元,那么该厂工人这一周的工资总额是多少元?