如右图,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0~180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P(a,a)点离开磁场.
求:
粒子在磁场中做圆周运动半径及速度;
粒子的比荷q/m;
从粒子发射到全部粒子离开磁场所用的时间.
如图(a)所示,“ ”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
”形木块放在光滑水平地面上,木块水平表面AB粗糙,光滑表面BC与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求: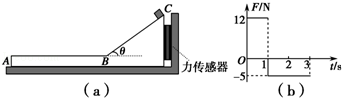
(1)斜面BC的长度;
(2)滑块的质量;
(3)运动过程中滑块发生的位移.
民用航空客机的机舱,除了有正常的舱门和舷梯连接,供旅客上下飞机外,一般还设有紧急出口.发生以外情况的飞机在着陆后,打开紧急出口的舱门,会自动生成一个由气囊构成的斜面,机舱中的人可沿该斜面滑行到地面上来,示意图如图所示设机舱出口离气囊底端的竖直高度h=3.0m,气囊构成的斜面长s=5.0m,CD段为斜面成平滑连接的水平地面,一个人从气囊顶端由静止开始滑下,人与气囊、人与地面间的动摩擦因数均为μ=0.5,不计空气阻力,g=10m/s2,求:
(1)人从斜坡上滑下时的加速度大小;
(2)人离开C点后在水平地面上滑行的距离.
如图甲所示,小球A从水平地面上P点的正上方h=1.8m处自由释放,与此同时,在P点左侧水平地面上的物体B在水平拉力的作用下从静止开始向右运动,B运动的v﹣t图象如图乙所示,且AB两物体均可看做质点,不考虑A球的反弹,g取10m/s2.求:
(1)小球A下落至地面所需的时间t;
(2)要使A、B两物体能够同时到达P点,求物体B的初始位置与P点的距离s.
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为m1和m2,各接触面间的动摩擦因数均为μ.重力加速度为g.
(1)当纸板相对砝码运动时,求纸板所受摩擦力的大小;
(2)要使纸板相对砝码运动,求所需拉力的大小;
(3)本实验中,m1=0.5kg,m2=0.1kg,μ=0.2,砝码与纸板左端的距离d=0.1m,取g=10m/s2.若砝码移动的距离超过l=0.002m,人眼就能感知.为确保实验成功,纸板所需的拉力至少多大?
民航客机一般都有紧急出口,发生意外情况的飞机紧急着陆后,打开紧急出口,狭长的气囊会自动充气,生成一条连接出口与地面的斜面,人员可沿斜面滑行到地上.若机舱口下沿距地面3.2m,气囊所构成的斜面长度为4.0m,一个质量为60kg的人沿气囊滑下时所受的阻力是240N.求:
(1)人下滑过程中的加速度为多大?
(2)人滑至气囊底端时速度有多大?