(本小题满分12分)
已知数列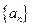 是等差数列,
是等差数列,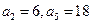 ;数列
;数列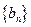 的
的 前n项和是
前n项和是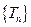 ,且
,且 .
.
(Ⅰ) 求数列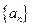 的通项公式;
的通项公式;
(Ⅱ) 求证:数列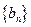 是等比数列;
是等比数列;
(Ⅲ) 记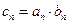 ,求
,求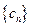 的前n项和
的前n项和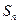 .
.
四棱锥P—ABCD中,底面ABCD是矩形,PA 底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
(I)求证:当N是BC边的中点时,MN∥平面PAC;
(Ⅱ)证明,无论N点在BC边上何处,都有PN AM;
AM;
(Ⅲ)当BN等于何值时,PA与平面PDN所成角的大小为45 .
.
甲、乙两同学进行下棋比赛,约定每局胜者得1分,负者得0分(无平局),比赛进行到有一个人比对方多2分或比满8局时停止,设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为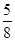 .
.
(I)如右图为统计这次比赛的局数n和甲、乙的总得分S,T的程序框图.其中如果甲获胜,输人a=l.b=0;如果乙获胜,则输人a=0,b=1.请问在①②两个判断框中应分别填写什么条件?
(Ⅱ)求p的值;
(Ⅲ)设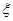 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量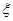 的分布列和
的分布列和

已知 ,数列
,数列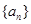 的首项
的首项
(1)求数列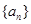 的通项公式;
的通项公式;
(2)设 ,数列
,数列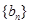 的前n项和为
的前n项和为 ,求使
,求使 的最小正整数n。
的最小正整数n。
设函数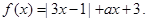
(1)若a=1,解不等式 ;
;
(2)若函数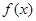 有最小值,求实数a的取值范围。
有最小值,求实数a的取值范围。
已知曲线C1的极坐标方程为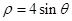 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为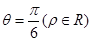 ,曲线C1,C2相交于点M,N。
,曲线C1,C2相交于点M,N。
(1)将曲线C1,C2的极坐标方程化为直角坐标方程;
(2)求线段MN的长。