(本小题满分14分)
设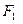 、
、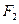 分别是椭圆
分别是椭圆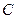 :
: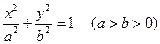 的左右焦点。
的左右焦点。
(1)设椭圆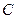 上点
上点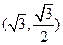 到两点
到两点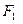 、
、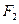 距离和等于
距离和等于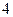 ,写出椭圆
,写出椭圆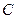 的方程和焦点坐标;
的方程和焦点坐标;
(2)设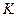 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段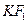 的中
的中 点
点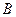 的轨迹方程;
的轨迹方程;
(3)设点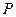 是椭圆
是椭圆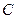 上的任意一点,过原点的直线
上的任意一点,过原点的直线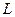 与椭圆相交于
与椭圆相交于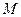 ,
,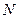 两点,当直线
两点,当直线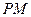 ,
,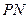 的斜率都存在,并记为
的斜率都存在,并记为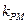 ,
,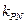 ,试探究
,试探究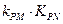 的值是否与点
的值是否与点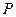 及直
及直 线
线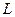 有关.
有关.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查,得到了如下的列联表:已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为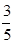 .
.
(1)请将上面的列联表补充完整;
(2)在多大的程度上可以认为性别与是否爱好打篮球有关系;
(3)已知喜爱打篮球的10位女生中,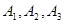 还喜欢打羽毛球,
还喜欢打羽毛球,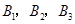 还喜欢打乒乓球,
还喜欢打乒乓球,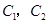 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求女生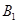 和
和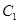 至少被选中一名的概率.
至少被选中一名的概率.
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计: |
50 |
已知二次函数y=f(x)的图像经过坐标原点,其导函数为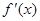 =6x-2,数列{
=6x-2,数列{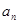 }的前n项和为
}的前n项和为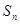 ,点(n,
,点(n,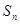 )(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{
)(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{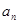 }的通项公式;
}的通项公式;
(Ⅱ)设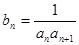 ,
,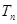 是数列{
是数列{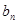 }的前n项和,求使得
}的前n项和,求使得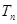 <对所有
<对所有
n∈N*都成立的最小正整数m;
已知函数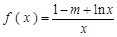 ,
,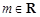 .
.
(Ⅰ)求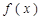 的极值;
的极值;
(Ⅱ)若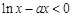 在
在 上恒成立,求
上恒成立,求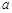 的取值范围.
的取值范围.
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值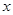 (单位:元,
(单位:元,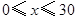 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成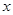 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
数列{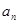 }满足
}满足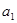 =1,
=1, =
=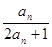 ,(1)计算
,(1)计算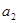 ,
, ,
,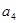 的值;
的值;
(2)归纳推测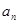 ,并用数学归纳法证明你的推测.
,并用数学归纳法证明你的推测.