棱长都相等的三棱锥的四个顶点都在同一外球面上,棱长为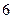 ;
;
(Ⅰ) 求此三棱锥的表面积;
(Ⅱ) 求此三棱锥的高;
(Ⅲ) 求此球的半径.
在曲线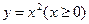 上有点A
上有点A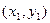 和点B
和点B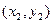 ,且
,且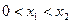 ,在A,B处的切线分别为
,在A,B处的切线分别为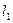 和
和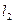 ,记
,记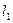 与曲线以及
与曲线以及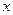 轴所围图形面积为
轴所围图形面积为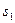 ,
,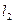 与曲线以及
与曲线以及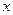 轴所围图形面积为
轴所围图形面积为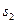 ,
,
(1)若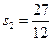 ,求过切点B的切线方程。
,求过切点B的切线方程。
(2)若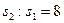 ,求
,求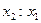 的值。
的值。
设函数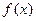 =
=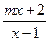 的图象的对称中心为点(1,1).
的图象的对称中心为点(1,1).
(1)求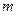 的值;
的值;
(2)若直线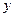 =
=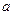 (
(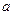 ∈R)与
∈R)与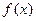 的图象无公共点,且
的图象无公共点,且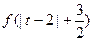 <2
<2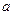 +
+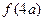 ,求实数
,求实数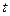 的取值范围.
的取值范围.
、已知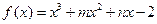 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称。
的图象关于y轴对称。
(1)求m,n的值及函数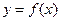 的单调区间;
的单调区间;
(2)若a>0,求函数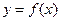 在区间
在区间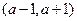 内的极值。
内的极值。
已知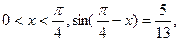 求
求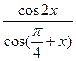 的值。
的值。
(14分)已知函数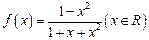 .
.
(1)求函数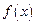 的单调区间和极值.
的单调区间和极值.
(2)若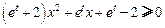 对满足
对满足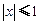 的任意实数
的任意实数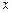 恒成立,求实数
恒成立,求实数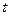 的取值范
的取值范
围(这里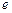 是自然对数的底数).
是自然对数的底数).
(3)求证:对任意正数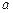 、
、 、
、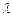 、
、 ,恒有
,恒有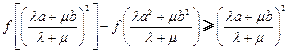
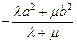 .
.