已知函数 图像上点
图像上点 处的切线与直线
处的切线与直线
平行(其中 ),
),
(I)求函数 的解析式;
的解析式;
(II)求函数 上的最小值;
上的最小值;
(III)对一切 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
P(x0,y0)(x0≠±a)是双曲线E: -
- =1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为
=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为 .
.
(1)求双曲线的离心率.
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足 =λ
=λ +
+ ,求λ的值.
,求λ的值.
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为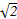 ,且过点P(4,-
,且过点P(4,-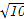 ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: ·
·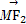 =0.
=0.
(3)求△F1MF2的面积.
已知椭圆C: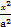 +
+ =1(a>b>0).
=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为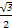 ,求椭圆的标准方程.
,求椭圆的标准方程.
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)过原点O任意作两条互相垂直的直线与椭圆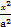 +
+ =1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
已知椭圆C: +
+ =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1, )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程.
(2)已知点Q( ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: ·
· 为定值.
为定值.
已知☉O:x2+y2=1和定点A(2,1),由☉O外一点P(a,b)向☉O引切线PQ,切点为Q,且满足|PQ|=|PA|.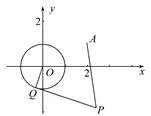
(1)求实数a,b间满足的等量关系.
(2)求线段PQ长的最小值.
(3)若以P为圆心所作的☉P与☉O有公共点,试求半径取最小值时☉P的方程.