一艘缉私巡逻艇在小岛A南偏西 方向,距小岛3海里的B处,发现隐藏在小岛边上的一艘走私船正开始向岛北偏西
方向,距小岛3海里的B处,发现隐藏在小岛边上的一艘走私船正开始向岛北偏西 方向行驶,测得其速度为10海里/小时,问巡逻艇需用多大的速度朝什么方向行驶,恰好用0.5小时在C处截住该走私船?
方向行驶,测得其速度为10海里/小时,问巡逻艇需用多大的速度朝什么方向行驶,恰好用0.5小时在C处截住该走私船?
(参考数据: )
)
(Ⅰ)把点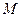
 的直角坐标化为极坐标;
的直角坐标化为极坐标;
(Ⅱ)求圆心在极轴上,且过极点和点 的圆的极坐标方程.
的圆的极坐标方程.
(本小题满分10分)选修4—5:不等式选讲。设正有理数 是
是 的一个近似值,令
的一个近似值,令 .
.
(I)若 ,求证:
,求证:
 ;
;
(II)求证: 比
比 更接近于
更接近于 .
.
(本小题满分10分)选修4—4:坐标系与参数方程。平面直角坐标系中,直线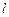
的参数方程是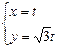 (
(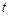 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,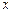 轴的正半轴为极轴,建立极坐
轴的正半轴为极轴,建立极坐
标系,已知曲线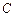 的极坐标方程为
的极坐标方程为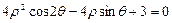 .
.
(I)求直线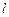 的极坐标方程;
的极坐标方程;
(II)若直线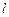 与曲线
与曲线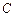 相交于
相交于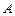 、
、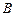 两点,求
两点,求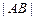 .
.
请考生在(22)、(23)、(24)三题中任选一题作答,如果多答,则按做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑.
(22)(本小题满分10分)选修4—1:几何证明选讲。如图,⊙O是△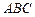 的外接圆,D
的外接圆,D
是的中点,BD交AC于E.
(I)求证:CD =DE·DB;
=DE·DB;
(II)若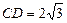 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径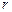 .
.
(本小题满分12分)已知函数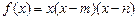 .
.
(I)当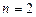 时,若函数
时,若函数 在
在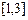 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(II)若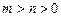 ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求 和
和 的值.
的值.