本小题满分10分)根据下列条件,求直线方程
(1)经过点A(3,0)且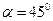
(2)经过点B(2,0),与C(0,-1)
(本小题满分12分)已知函数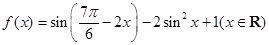 ,
,
(Ⅰ)求函数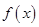 的周期及单调递增区间;
的周期及单调递增区间;
(Ⅱ)在 中,三内角
中,三内角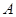 ,
, ,
,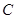 的对边分别为
的对边分别为 ,已知函数
,已知函数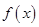 的图象经过点
的图象经过点 成等差数列,且
成等差数列,且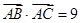 ,求
,求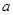 的值.
的值.
(本小题满分l4分)已知函数 .
.
(Ⅰ)当a=0时,求 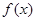 的极值;
的极值;
(Ⅱ)当a<0时,求 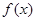 的单调区间;
的单调区间;
(Ⅲ)方程 的根的个数能否达到3,若能请求出此时a的范围,若不能,请说明理由,
的根的个数能否达到3,若能请求出此时a的范围,若不能,请说明理由,
(本小题满分13分)如图,椭圆 的离心率为
的离心率为 ,x轴被曲线
,x轴被曲线  截得的线段长等于
截得的线段长等于 的短轴长,
的短轴长,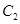 与y轴的交点为M,过坐标原点O的直线
与y轴的交点为M,过坐标原点O的直线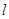 与
与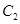 相交于点A、B,直线MA,MB分别与
相交于点A、B,直线MA,MB分别与 相交于点D、E.
相交于点D、E.
(Ⅰ)求 、
、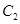 的方程;
的方程;
(Ⅱ)求证:MA MB:
MB:
(Ⅲ)记 MAB,
MAB, MDE的面积分别为
MDE的面积分别为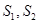 ,若
,若  ,求
,求 的最小值.
的最小值.
(本小题满分12分)数列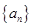 的前n项和记为
的前n项和记为  ,等差数列
,等差数列 的各项为正,其前n项和为
的各项为正,其前n项和为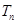 ,且
,且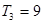 ,又
,又 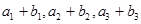 成等比数列.
成等比数列.
(Ⅰ)求 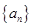 ,
, 的通项公式;
的通项公式;
(Ⅱ)求证:当n  2时,
2时,
(本小题满分12分)一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为l,2,3,4,5:4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(Ⅰ)求取出的3个球编号都不相同的概率;
(Ⅱ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望