（本小题满分12分）一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为l，2，3，4，5：4个白球编号分别为1，2，3，4，从袋中任意取出3个球．
（Ⅰ）求取出的3个球编号都不相同的概率；
（Ⅱ）记X为取出的3个球中编号的最大值，求X的分布列与数学期望
（如图所示，在四棱锥P—ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.
（1）求证：PB⊥DM；
（2）求BD与平面ADMN所成的角.
（在正四面体P—ABC中,D,E,F分别是AB、BC、 CA的中点,求证: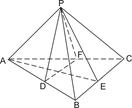
（１）BC∥平面PDF;（２）BC⊥平面PAE
(本题12分) 设函数
．
(1) 求函数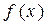
的单调区间；
(2) 若函数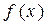在区间(0,2)上单调递减，试求实数
的取值范围；
(3) 若函数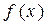的极小值大于0，试求实数的取值范围．
(本题12分)口袋里放了12个大小完全一样的小球，其中3个是红色的，
4个是白色的，5个是蓝色的，现从袋中任意取出4个小球，求：
(1) 取出的小球的颜色至少是两种的概率；
(2) 取出的小球的颜色是三种的概率．
（本题12分）七个人排成两排照相，前排3人，后排4人．
(1) 求甲在前排，乙在后排的概率；
(2)求甲、乙在同一排且相邻的概率；
(3) 求甲、乙之间恰好有一人的概率．