已知:以点C (t, )(t∈R , t≠ 0)为圆心的圆与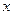 轴交于点O, A,与y轴交于点O, B,其中O为原点
轴交于点O, A,与y轴交于点O, B,其中O为原点
(1)求△OAB的面积的值
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程
已知点P在圆x2+y2=1上运动,过点P作x轴的垂线,垂足为D,点M在DP的延长线上,且有|DP|=|MP|.(1)求M点的轨迹方程C;(2)已知直线l过点(0,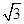 ),且斜率为1,求l与C相交所得的弦长.
),且斜率为1,求l与C相交所得的弦长.
如图所示,在四棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
已知数列{an}是等差数列,且a3=5,a2+a7=16.
(1)求数列{an}的通项公式;
(2)设bn=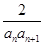 ,求数列{bn}的前
,求数列{bn}的前 项和Sn.
项和Sn.
已知函数f(x)=log4(2x+3-x2).
(1)求f(x)的定义域;
(2) 求f(x)的单调区间.
已知函数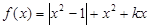 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程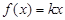 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数 的取值范围;
的取值范围;
(3)若关于x的方程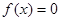 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解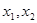 ,求k的取值范围。
,求k的取值范围。