(本小题满分12分)
《中华人民共和国个人所得税》规定,公民全月工资所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额。此项税款按 下表分段累计计算:
下表分段累计计算:
| 全月应纳税所得额 |
税率(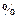 ) ) |
| 不超过500元的部分 |
5 |
| 超过500元至2000元的部分 |
10 |
| 超过2000元的部分 |
15 |
(1)求某人当月所交税款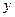 元关于其当月工资
元关于其当月工资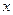 元的函数
元的函数
(2)若某人某月所交税款为26.78元,求当月的工资
(3)若某人当月的工资收入在3000元至6000元之间,求该月所交税款的范围
设 为奇函数,
为奇函数, 为常数。
为常数。
(1)求 的值;
的值;
(2)证明: 在(1,+∞)内单调递增;
在(1,+∞)内单调递增;
(3)若对于[3,4]上的每一个 的值,不等式
的值,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
如图,在直三棱柱 中,
中, ,
,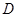 为
为 中点.
中点.
(1)求证: ;
;
(2)求证:  ∥平面
∥平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
(12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为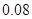 ,只选修甲和乙的概率是
,只选修甲和乙的概率是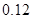 ,至少选修一门的概率是
,至少选修一门的概率是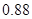 ,用
,用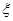 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)求学生小张选修甲的概率;
(Ⅱ)记“函数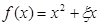 为
为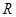 上的偶函数”为事件
上的偶函数”为事件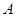 ,求事件
,求事件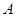 的概率;
的概率;
(Ⅲ)求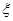 的分布列和数学期望;
的分布列和数学期望;
(12分)已知各项均为正数的数列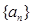 的前n项和为
的前n项和为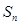 ,且
,且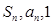 成等差数列.
成等差数列.
(1)求数列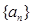 的通项公式;
的通项公式;
(2)若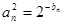 ,设
,设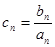 求数列
求数列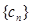 的前项和
的前项和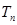 .
.
设函数 ,其中向量
,其中向量 ,
,
(1)求 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中, 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的值。
的值。