设函数 ,其中向量
,其中向量 ,
,
(1)求 的最小正周期与单调减区间;
的最小正周期与单调减区间;
(2)在△ABC中, 分别是角A、B、C的对边,已知
分别是角A、B、C的对边,已知 ,△ABC的面积为
,△ABC的面积为 ,求
,求 的值。
的值。
如图, 是长方形海域,其中
是长方形海域,其中 海里,
海里,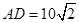 海里.现有一架飞机在该海域失事,两艘海事搜救船在
海里.现有一架飞机在该海域失事,两艘海事搜救船在 处同时出发,沿直线
处同时出发,沿直线 、
、 向前联合搜索,且
向前联合搜索,且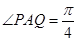 (其中
(其中 、
、 分别在边
分别在边 、
、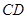 上),搜索区域为平面四边形
上),搜索区域为平面四边形 围成的海平面.设
围成的海平面.设 ,搜索区域的面积为
,搜索区域的面积为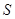 .
.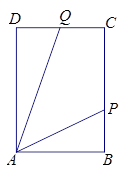
(1)试建立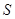 与
与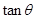 的关系式,并指出
的关系式,并指出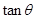 的取值范围;
的取值范围;
(2)求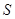 的最大值,并指出此时
的最大值,并指出此时 的值.
的值.
数列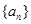 的前
的前 项和为
项和为 ,满足
,满足 .等比数列
.等比数列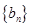 满足:
满足: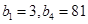 .
.
(1)求证:数列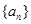 为等差数列;
为等差数列;
(2)若 ,求
,求 .
.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1)求角A的大小;
(2)若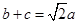 ,
, 的面积
的面积 ,求
,求 的长.
的长.
已知 的三个顶点的坐标为
的三个顶点的坐标为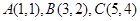 .
.
(1)求边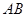 上的高所在直线的方程;
上的高所在直线的方程;
(2)若直线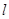 与
与 平行,且在
平行,且在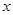 轴上的截距比在
轴上的截距比在 轴上的截距大1,求直线
轴上的截距大1,求直线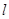 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
设数列 的首项
的首项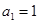 ,前
,前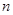 项和为
项和为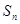 ,且
,且 ,
,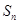 ,
,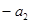 成等差数列,其中
成等差数列,其中 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 满足:
满足: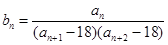 ,记数列
,记数列 的前
的前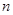 项和为
项和为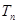 ,求
,求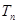 及数列
及数列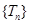 的最大项.
的最大项.