在直角坐标系 中,曲线C1的参数方程为 (t为参数, ).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线 .
(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(Ⅱ)直线C3的极坐标方程为 ,其中α0满足 ,若曲线C1与C2的公共点都在C3上,求a.
(本题12分)
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD, AP="AB," BP=BC=2,E,F分别是PB,PC的中点
(1)证明:EF 面PAD
面PAD
(2)求三棱锥E-ABC的体积
(本题12分)
为调查某地区老年人是否需要志愿者提供帮助用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 男 |
女 |
|
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中需要志愿者提供帮助的老年人的比例
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:
 |
0.050 |
0.010 |
0.001 |
 |
3.841 |
6.635 |
10.828 |
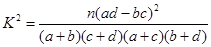
.(本题12分)函数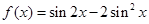
(1)求函数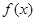 的最小正周期
的最小正周期
(2)求函数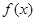 的最大值及
的最大值及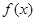 取得最大值时
取得最大值时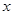 的取值集合
的取值集合
已知函数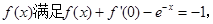 函数
函数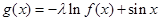 是区间
是区间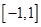 上的减函数. ①当
上的减函数. ①当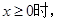 曲线
曲线 在点
在点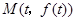 的切线
的切线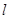 与
与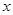 轴、
轴、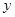 轴围成的三角形面积为
轴围成的三角形面积为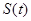 ,求
,求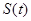 的最大值;
的最大值;
②若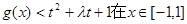 时恒成立,求t的取值范围;
时恒成立,求t的取值范围;
③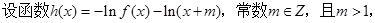 试判定函数
试判定函数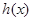 在区间
在区间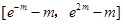 内的零点个数,并作出证明.
内的零点个数,并作出证明.
已知函数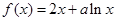
①若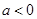 ,对于任意两个正数
,对于任意两个正数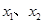 ,试判定
,试判定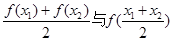
的大小;②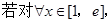
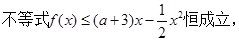 求实数
求实数 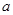 的取值范围.
的取值范围.