(本小题满分12分)如图,四边形 与
与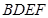 均为菱形,
均为菱形, 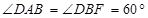 ,且
,且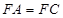 ,
,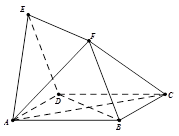
(Ⅰ)求证: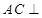 平面
平面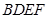 ;
;
(Ⅱ)求证:AE∥平面FCB;
(Ⅲ)求二面角 的余弦值。
的余弦值。
(本小题满分10分)若直线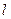 与直线
与直线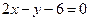 平行,且与坐标轴围成的三角形面积为16,求直线
平行,且与坐标轴围成的三角形面积为16,求直线 的方程。
的方程。
(本小题满分14分)
已知a∈R,函数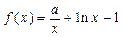 ,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在
,g(x)=(lnx-1)ex+x(其中e为自然对数的底数).(1)判断函数f(x)在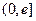 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数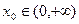 ,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
,使曲线y=g(x)在点x=x0处的切线与y轴垂直? 若存在,求出x0的值;若不存在,请说明理由.(3)若实数m,n满足m>0, n>0,求证:nnem≥mnen.
(本小题满分13分) 已知A、B、C是椭圆
已知A、B、C是椭圆 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为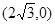 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且 .
.
(1)求椭圆m的方程;
(2)过点 的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且
的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且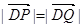 .求实数t的取值范围.
.求实数t的取值范围.
(本小题满分12分)
右图是某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S、D、A、Q及P、D、C、R共线.(Ⅰ)沿图中虚线将它们折叠起来,使P、Q、R、S四点重合为点P,请画出其直观图;(Ⅱ)求二面角P-AB-D的大小;(Ⅲ)试问需要几个这样的几何体才能拼成一个棱长为6的正方体ABCD-A1B1C1D1?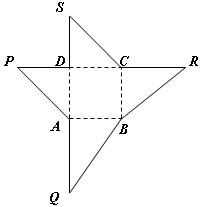
(本小题满分12分)
在数列{an}中,a1=2,a2=8,且已知函数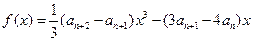 (
(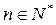 )在x=1时取得极值.(Ⅰ)求证:数列{an+1—2an}是等比数列,(Ⅱ)求数列
)在x=1时取得极值.(Ⅰ)求证:数列{an+1—2an}是等比数列,(Ⅱ)求数列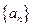 的通项an;(Ⅲ)设
的通项an;(Ⅲ)设 ,且
,且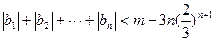 对于
对于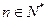 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.