(本小题满分12分)设函数 (
( 为常数).
为常数).
(1)当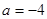 时,证明
时,证明 在[1,+∞)上是单凋递增函数;
在[1,+∞)上是单凋递增函数;
(2)若函数 有两个极值点
有两个极值点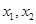 ,且
,且 ,求证:
,求证: .
.
设X~N(5,1),求P(6<X<7).
某市有210名初中学生参加数学竞赛预赛,随机调阅了60名学生的答卷,成绩列表如下:
| 成绩 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 人数分布 |
0 |
0 |
0 |
6 |
15 |
21 |
12 |
3 |
3 |
0 |
(1)求样本的数学平均成绩及标准差;(精确到0.01)
(2)若总体服从正态分布,求此正态曲线的近似方程.
设X~N(10,1).
(1)证明:P(1<X<2)=P(18<X<19);
(2)设P(X≤2)=a,求P(10<X<18).
工厂制造的某机械零件尺寸X服从正态分布N(4, ),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
),问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围的零件大约有多少个?
设X~N(1,22),试求
(1)P(-1<X≤3);
(2)P(3<X≤5);
(3)P(X≥5).