已知等差数列 的前n项和为Sn,等比数列 的前n项和为Tn, , , .
(1)若 ,求 的通项公式;
(2)若 ,求S3.
(本小题满分12分)
在直三棱柱 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,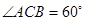 ,E、F分别是
,E、F分别是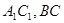 的中点。
的中点。
(1)证明:平面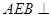 平面
平面 ;
;
(2)证明: 平面ABE;
平面ABE;
(3)设P是BE的中点,求三棱锥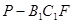 的体积。
的体积。
(本小题满分10分)
已知向量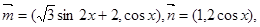 设函数
设函数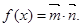
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中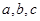 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若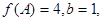 △ABC的面积为
△ABC的面积为 ,求
,求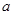 的值.
的值.
.(本题满分12分)
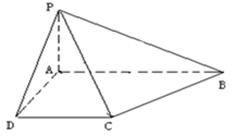
已知四棱锥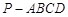 的底面为直角梯形,
的底面为直角梯形, //
// ,
,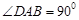 ,
,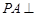 底面
底面 ,且
,且 .
.
(1)证明: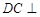 平面
平面 ;
;
(2)求二面角 的余弦值的大小.
的余弦值的大小.
(本题满分12分)
已知椭圆的中心在原点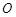 ,焦点在坐标轴上,直线
,焦点在坐标轴上,直线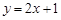 与该椭圆相交于
与该椭圆相交于 和
和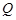 ,且
,且 ,
, ,求椭圆的方程.
,求椭圆的方程.
(本题满分12分)设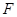 为抛物线
为抛物线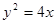 的焦点,
的焦点,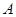 为抛物线上任意一点,已
为抛物线上任意一点,已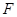 为圆心,
为圆心,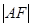 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于 点,试判断过
点,试判断过 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。