.(本题满分12分)
已知四棱锥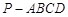 的底面为直角梯形,
的底面为直角梯形, //
// ,
,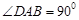 ,
,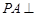 底面
底面 ,且
,且 .
.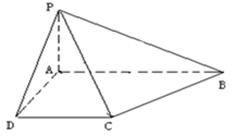
(1)证明: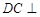 平面
平面 ;
;
(2)求二面角 的余弦值的大小.
的余弦值的大小.
(本小题满分12分)已知数列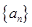 的前
的前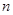 项和为
项和为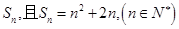 .
.
(Ⅰ)求数列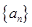 的通项公式;
的通项公式;
(Ⅱ)设集合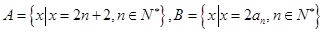 ,等差数列
,等差数列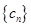 的任一项
的任一项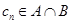 ,其中
,其中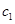 是
是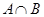 中的最小数,
中的最小数,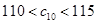 ,求数列
,求数列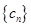 的通项公式.
的通项公式.
(本小题满分12分)甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(Ⅰ)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(Ⅱ)若左右手依次各取两球,称同一手中 两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列和数学期望.
(本小题满分12分)直三棱柱 中,
中,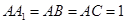 ,E,F分别是
,E,F分别是 的中点,
的中点,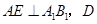 为棱
为棱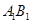 上的点.
上的点.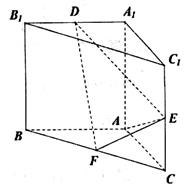
(Ⅰ)证明: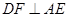 ;
;
(Ⅱ)已知存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ,请说明点D的位置.
,请说明点D的位置.
(本小题满分12分)在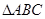 中,已知
中,已知 .
.
(Ⅰ)求sinA与角B的值;
(Ⅱ)若角A,B,C的对边分别为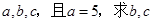 的值.[
的值.[
在自然数列 中,任取
中,任取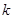 个元素位置保持不动,将其余
个元素位置保持不动,将其余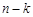 个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为
个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为 .
.
(1)求 ;
;
(2)求 ;
;
(3)证明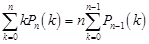 ,并求出
,并求出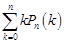 的值.
的值.